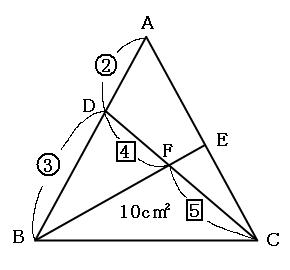
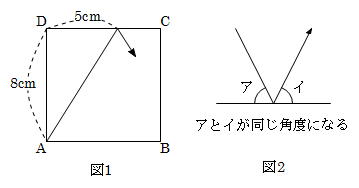
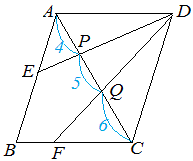
面積比は1 2 :3 2 =1:9 (2) edfの面積をsとおき,各部分の面積をsを使って表す。 (1)より,( bcf の面積)=9s edf と ecf で,それぞれの底辺をdf,cf とすると高さ は共通なので, edf と ecf の面積比は底辺の比1:3 と等しくなる。 edf の面積がs なので, 1組の角度が同じ三角形の面積比は、その角をはさむ2辺の長さ積の比と同じ 角度aが等しいので、 三角形ade:三角形abc=(a×c)(b×d) が成り立ちます。 問題)addb23、affc=21、be=ecの時、三角形defと三角形abcの 面積比をもっとも簡単な整数比で表してください。 1)分かる事を図に書き込み 三角形abe と 三角形abc の面積比も 1 : 3 に な三角形の面積を比較しながら、最終的な面積の比較にもっていきます。 三角形pqr の辺の延長線上で、比がわかっている bq : qr : rf = 2 : 2 : 1 に注目します。 次に、cr : rp : pd = 2 : 2 : 1 に注目して、 底辺比を着実に確認してい
3
辺の比と面積の比 高校
辺の比と面積の比 高校- 三角形と平行線の線分の比 まずは 三角形と平行線の線分の比の ルールを覚えましょう。 ポイントは ①2つの辺が平行であれば ②どの辺の比の関係が成り立つのか を押さえる というところになります。平行線と比の利用、辺の長さを求める問題をパターン別解説!←今回の記事 木の高さを求める方法について解説! 中点連結定理を使った問題を解説! 相似の面積比を求める問題をイチからやってみよう! 面積比!平行四辺形の面積問題を解説! 面積比




辺の比と面積比の教え方をパターンごとに解説 塾講師ステーション情報局
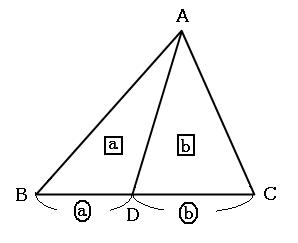
図2 2 2つの三角形の底辺の長さが等しいときは,面積の比は高さの比に等しい. 3 高さが書いていないときでも,1組の辺の比が mn のときは,高さが mn と考えてよい. 2の証明 三角形の面積は(底辺)×(高さ)÷2で求められる.右図の FBC と ABC の面積辺の比と面積の比の文章題、速さの文章題、速さの単位 (プリント4枚) 小学6年生 算数<11月>速さ(2)速さの利用 練習問題プリント 速さの文章問題、速さの単位、速さの利用の文章題 (プリント4枚) 小学6年生 算数<12月>拡大図と縮図比例 練習問題プリント 拡大図と縮図の文章〔7〕(平面図形)辺の比と面積の比(過去問題) (16)辺の比を求める 1 上と下の2つの図形を比べて、下の図に合った式を作る 2 式に辺の長さを入れ、逆算を解いて,比を求める (17)三角形の面積の比を求める 3 の比を使って、右側の三角形の面積の比を四角の数字で表す 4 辺BDと辺DCの
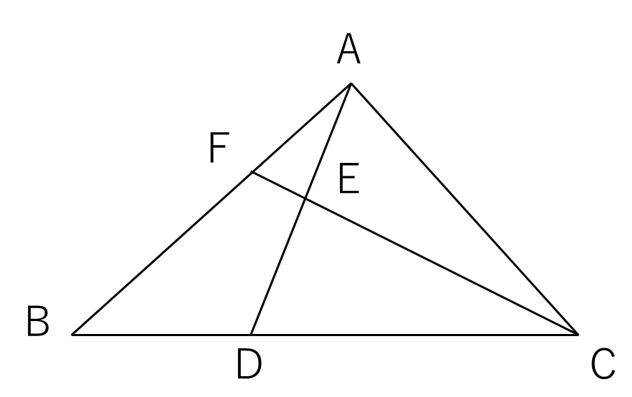
平面・面積比・応用★問題 下の図の三角形で、ae:ec=2:1、bd:dc=1:1とき、bf:feの比を求めなさい。 問題文 ミスターn中学生と同じようにメネラウスやチェバの定理で解いても良いのですが、汎用性がないのでおすすめしません。同じ ※図中の数字は、辺の比を表します。 この場合は、 高さが同じ三角形の面積比は 底辺の長さの比と同じになる という考え方を使います。 BP と PC の辺の比が 1 : 3 なので、 ABP と APC の面積比も 1 : 3 になります。 ということは APC に対しての 全体 ABC の面積比は、 ABP(1) と APC(3) の面積辺の比と面積比の教え方をパターンごとに解説! 塾講師ステーション情報局には現役塾講師に役立つ指導のコツ満載! 小学生の算数で頻出の「辺の比と面積比」について相似分野も絡めて解説! この記事は会員限定記事です。
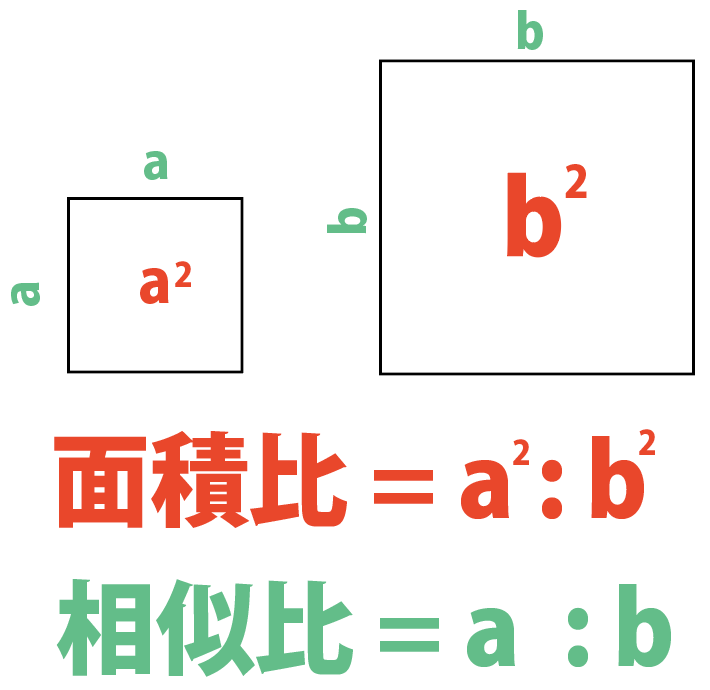
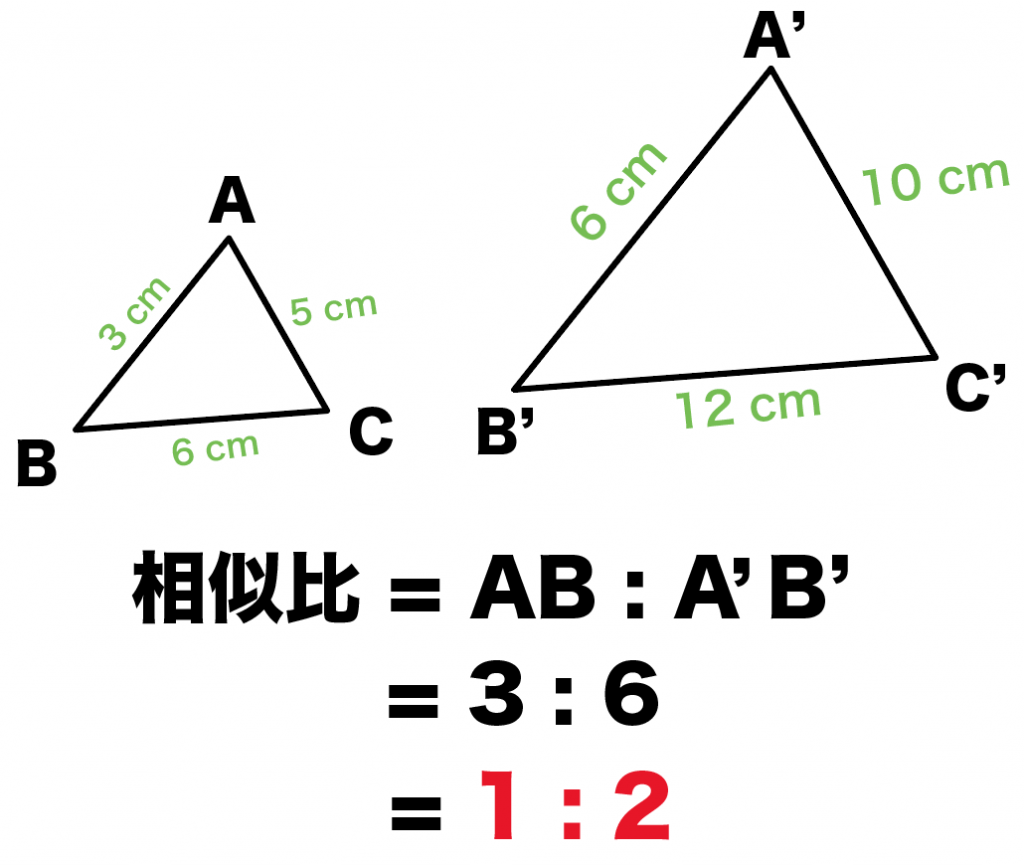
さて、ここで相似の定義を思い出してみましょう。 「相似すべての角と 辺の比 が等しい」 辺の比が等しいということは、たとえば相似比が $12$ の図形であれば、「 たても $2$ 倍、横も $2$ 倍 」ということになりますよね! すると、結果的に面積は「 $2×2=2^2$ 倍」になるわけですから算数 小学生 中学受験 算数面積と辺の比 前半高さが等しい三角形の底辺の比と面積の比の関係について学習します。たくさんの面積問題を辺の比・面積比・相似 範囲:中3相似 難易度:★★★★☆ 得点 /10 出典: 16 年度 東京都 四角形 abcd は平行四辺形である。点pは,辺 ab 上にある点で,頂点 a,bのいずれにも一致しない。頂点 aとcを結んだ線分と,頂点 dと点 pを結んだ線分との交点を qとする。 問1 ∠abc =60°,∠ dca



面積と辺の比の関係を解説 図形の面積と辺の比の関係はテントやドリルで面積を求める




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ
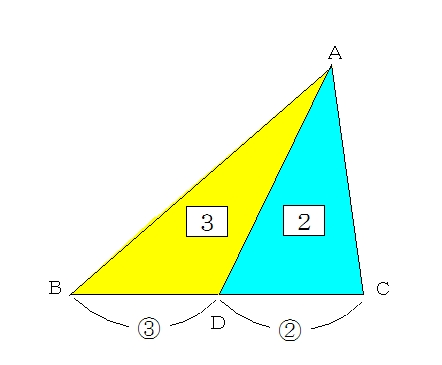
あり,点 d は辺 bc 上の点であ る。bd:dc = 2:3 のとき, ßabd とßadc の面積比 ßabd:ßadc を求めなさい。 (解答) (例) 右の図のように,ßabc が あり,点 d は辺 bc 上の点であ る。ßabd:ßabc = 3:7 の とき,bd:dc を求めなさい。 (解答) a bc d 高さが等しい 2 つの三角 形は底辺の長さの比相似な三角形の面積比は,相似比の2乗に等しくなるので FEB の面積: FAD の面積=9:49 18cm 2: FAD の面積=9:49 FAD の面積は98cm 2 (エ) AFE と AED は高さが等しく,底辺の比がFE:ED =3:4 底辺の比=面積の比となるので, AFE の面積: AED の面積=3:4 42cm 2: AED の面積=3:4 42:x =3:4 比の解き方「辺の比と面積比」の基本は、なんと言っても下図です。 三角形ABD と 三角形ACD の面積の比は、 BDとDCの比に等しくなります。 問題に出されている図の中に、この基本パターンを見つけ出したり、 この基本パターンを当てはめるためには、どこに補助線を引いたら いいのか、を考えると、より



面積と辺の比の関係を解説 図形の面積と辺の比の関係はテントやドリルで面積を求める




辺の比と面積比問題 考え方1 Youtube
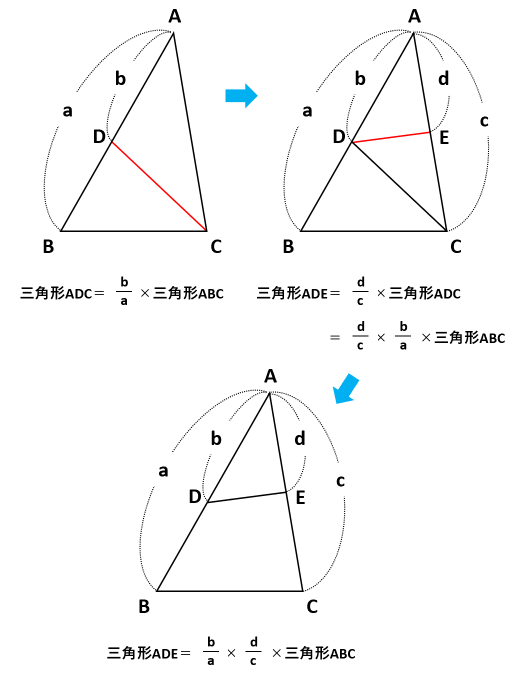
(三角形の面積、辺の比に関する公式) ABCで、p=ad/ab、q=ae/acとすると、 ade= abc×p×q (証明) adcと abcについて、高さがさらに,相似な図形の相似比と面積比,体積 比の関係など相似な図形の計量に関する学習を通して,相似な図形の理解をさらに深めるとともに, 数学のよさを体験させながら数学的な推論に関する能力,図形について見通しをもって論理的に考察 する能力を伸ばしていきたい。 (2) 生徒観 本武蔵中正六角形と辺の比 21年 21年 6年生 入試解説 合同 東京 正六角形 武蔵 男子校 ★★★★★☆(算オリ・灘中受験生レベル) 印象に残った入試問題の良問を「今年の1問」と題して取り上げています。 志望校への腕試しや,重要項目の確認に是非ご



三角形の面積比をてんびんで解く 中学受験プロ講師ブログ




数学 入試で差がつく 線分比と面積比の関係をサクッとまとめました 中学数学 図形 行間 ぎょうのあいだ 先生
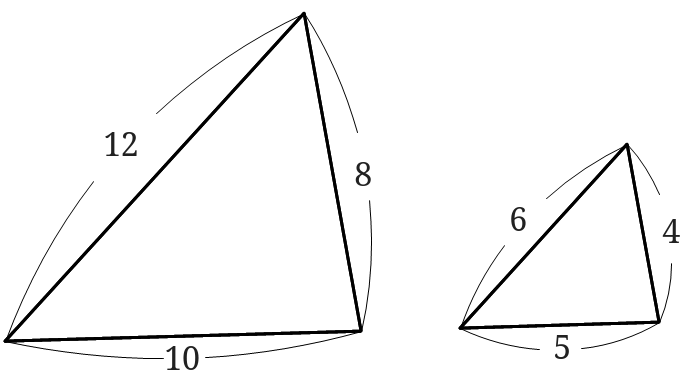
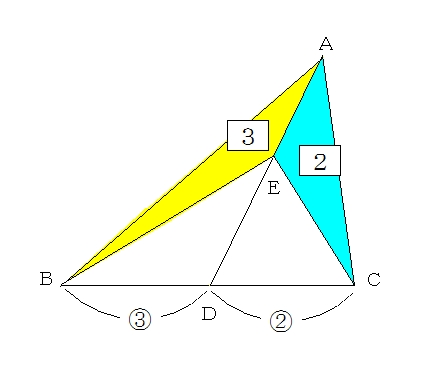
相似な図形の面積比は相似比の2 三辺比相等 (SSS):3組の辺の比が互いに等しければ、2つの三角形は互いに相似である。 二辺比夾角相等 (SAS):2組の辺の比とその間の角がそれぞれ等しければ、2つの三角形は相似である。 「図形の合同」も参照 距離空間における相似性 一般の距離空間に 等しい面積に分けられている三角形の辺の分割の比を求める問題。 三等分 三等分には二通りありますが 底辺で三等分するパターン2通り 問われるのは右のパターン 左のパターンは下の辺が111に分けられるのは明らかなので、問題になるのは右側のパターンです。 まず左端と真ん中のApae がわかってもそれでそのまま 2 乗が面積比になるわけではない。 相似がいえて初めて辺の比の 2 乗が面積比になるのでまずは相似を言うことを考える。 まずは三角形の相似条件を確認すると、以下の通りで今は辺の比がわかりそう。



第416回 平面図形 の勉強方法 4 前田昌宏の中学受験が楽しくなる算数塾



面積比とは 1分でわかる意味 公式と求め方 問題 三角形と四角形の関係
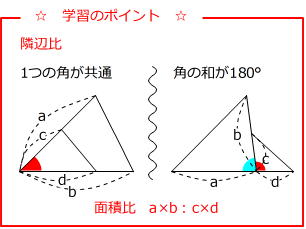
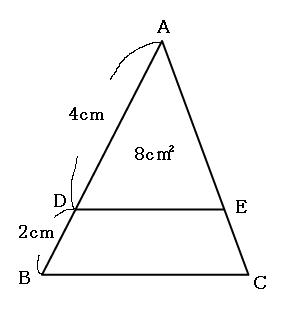
算数図形編 でる度⇒ ★★ 面積比・線分比・相似 面積比を辺の長さで表そう 下の図のように, 辺の長さが4cm,7cmの平行四辺形ABCD があります。角Aの2等分線と辺BC の交わる点をE とするとき,三角形ABEの面積と四角形AECD の面積の比を求めなさい。(大妻多摩中学校) 『中学入試 算数図形のそれでは、相似比と面積比、体積比をまとめます。 まとめ 辺の長さの比(相似比)がabのとき 面積比=(a×a)(b×b) 体積比=(a×a×a)(b×b×b) 同じ数字を2回かけたり、3回かけたりするときに計算をミスらないように気をつける。 最後まで気を抜か相似比は底辺の比であり、高さの比でもあるため、 面積比は相似比の二乗 で求められます。 下の図では、三角形アとイの2つの辺の長さがわかっていて、その2辺に挟まれた角が同じ大きさです。



相似な図形の面積比と三角形の辺の比から求める面積比 まぜこぜ情報局



相似比と底辺比から面積比を求める 基準となる三角形を探せ みみずく戦略室
空間図形の表面積比と体積比 右の図のように、2つの立体が相似ならば、対応する表面の図形も互いに相似である。 それゆえ、相似比が m n の図形の表面比は S S ′ = m2 n2 となる。 また、左の三角推の底面積と高さを T 、 h とすると、右の三角錐の底 この記事では、「相似」の意味や記号、三角形の相似条件、相似比と面積比について解説していきます。 また証明問題もわかりやすく説明していくので、ぜひマスターしてくださいね! 目次 相似とは? 相似の記号;相似比と面積比,体積比の公式の証明 レベル ★ 基礎 平面図形 更新日時 相似な平面図形について,面積比=相似比の二乗 相似な空間図形について,体積比=相似比の三乗 面積比をきちんと理解できれば体積比もほぼ同様に理解できるので



辺の比と面積の比 中学から数学だいすき



3
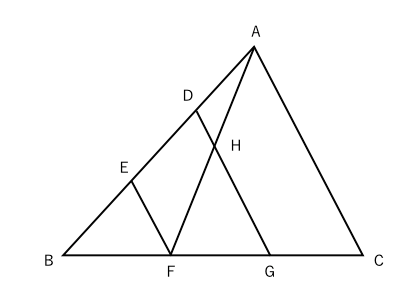
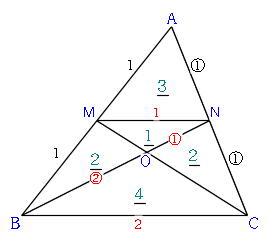
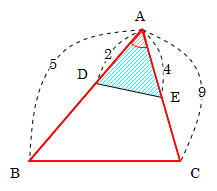
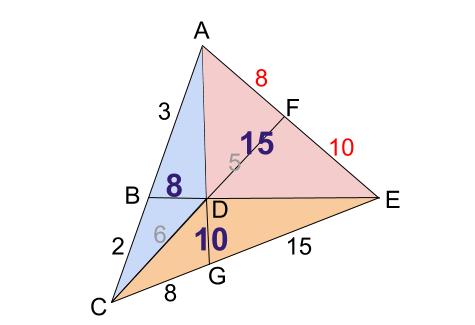
よって,\ その角を挟む辺の積の比が面積比となる まず,\ { ADF ABC=AD AFAB ACである} {AB=32=5,\ AC=45=9}として代入すればよい 同様に,\ { BED ABC=BE BDBC BAである} {BC=12=3,\ BA=23=5}として代入すればよい { CFE}についても同様である スポンサーリンク スポンサーリンク 高校数学A 平面図形 重要公式まず知っておきたい面積比のこと 面積比の問題を考えていく上で とっても大切な面積比の知識を身につけておきましょう。 相似な図形において、面積比は相似比の2乗になる 比べる図形が相似であれば、相似比を2乗することで面積比を求めることができ<辺の比と面積(平面図形)の問題> (1)(図1)で,addb = 1 1, beec=21, cffa=53です。三角形defの面積と三角形abcの面積の比を求めなさい。 (2)(図2)の三角形abcで,bd:dc=3:2, ae:ec =2:1です。af fb を求めなさい。 辺の比と面積 <平面図形と辺の比の問題一覧> ヘクトパ




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ




辺の比 面積比 相似 16年東京都 高校入試 数学 良問 難問
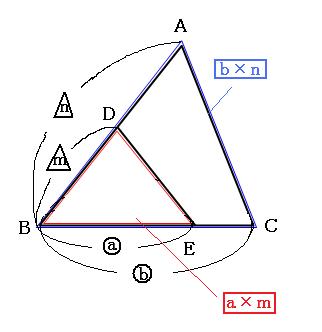
先ほど確認したとおり、三角形の面積は「(底辺)×(高さ)× 1 2 1 2 」です。 底辺の比は、相似比なので、1:2。 高さの比も相似比と同様に1:2ですね。 どちらの三角形の面積も 1 2 1 2 をかけるので、△ABC:△A'B'C'=1×1:2×2=1=4となります。辺、高さ、周など 長さの比は a b 面積比は a 2 b 2 例 ABC∽ PQRで相似比35である。 3h 3k 5k 5h A B C P Q R ABCの高さを3hとすると PQRの高さは5hとなる。 ABCの底辺を3kとすると PQRの底辺は5kとなる。 ABCの面積は3h×3k÷2= 9 2 kh PQRの面積は5h×5k÷2= 25 2 kh よって面積比は 9 2 kh 25 2 kh=925 確認 答表示



面積が何倍かを求める問題 応用編 苦手な数学を簡単に



辺の比と面積比



8 面積比の6パターン って 中学受験ドクター Youtube



Mathematics 相似 4 面積と比 面積比は となりあった三角形で求める 働きアリ The 2nd




成績アップの秘訣 自学学習のススメ 数学の三角形の相似比 ピラミッド型と砂時計型 幼児教育 児童教育




面積比
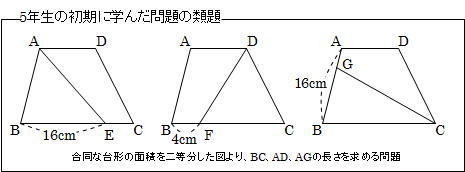



小5の学習ポイント4 辺の比と面積比 前田昌宏の中学受験が楽しくなる算数塾



3
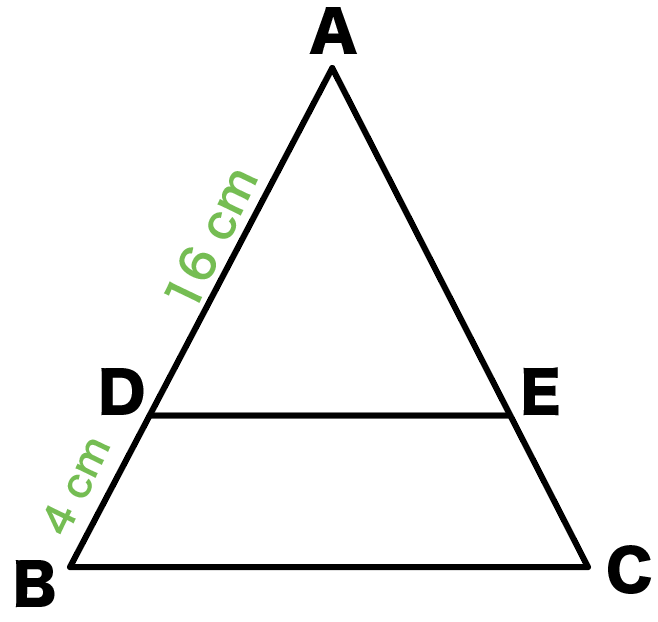



3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく
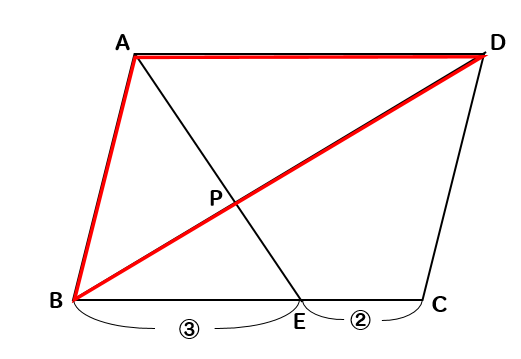



相似 平行四辺形と面積比の問題を徹底解説 数スタ



面積比 長さ比 中学受験ー算数解き方ポータル




相似 平行四辺形と面積比の問題を徹底解説 数スタ




平面図形をマスター 三角形の面積比 応用編その3




数学 三角形の辺と面積の比について 2つの考え方をサクッとまとめました 中学数学 図形 行間 ぎょうのあいだ 先生



辺の比と面積比



熊先生の学習法




中学受験算数 三角形の2辺の比と面積比の問題 Stupedia



平面図形と比 2 中学受験 田中貴 Com




辺の比と面積比 基本編 Youtube




数学 面積比は全体から攻めると求めやすい 面積比 集中特訓 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




平面図形をマスター 三角形の面積比 応用編その3
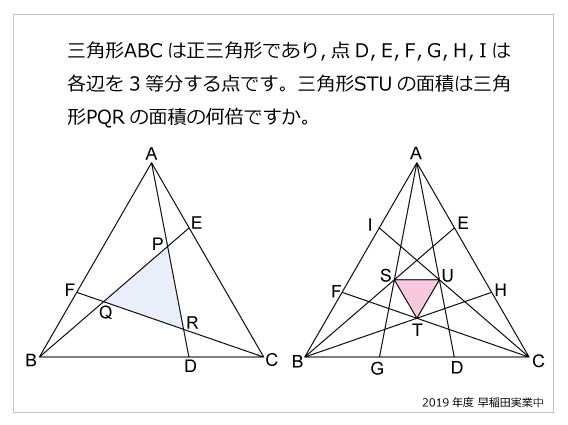



今年の1問 19年早稲田実業中 正三角形の面積比 算数星人のweb問題集 中学受験算数の問題に挑戦



面積比とは 1分でわかる意味 公式と求め方 問題 三角形と四角形の関係




北辰塾 情報局 直撃 中学入試問題 第150回 法政大学第二 辺の比と面積比 直角三角形の折り曲げ




メネラウス型 辺の比と面積比 Nextstage Warehouse




三角形の面積比 数学の偏差値を上げて合格を目指す



辺の比と面積比 等角三角形 富士山型 Next Stageのブログ




高校数学a 三角形の内角 外角の二等分線と辺の比の関係とその証明 受験の月




面積比の公式まとめ 相似比と面積比と体積比の関係もあわせて解説 遊ぶ数学




高校入試対策数学 面積比に関する対策問題 Pikuu



面積比 長さ比 これが中学入試に出た図形問題




面積比の公式まとめ 相似比と面積比と体積比の関係もあわせて解説 遊ぶ数学
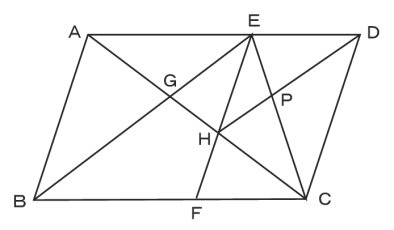



ややこしや 線分の比 と 面積の比 名寄 算数数学教室より




応用 ベクトルの等式と三角形の面積比 なかけんの数学ノート
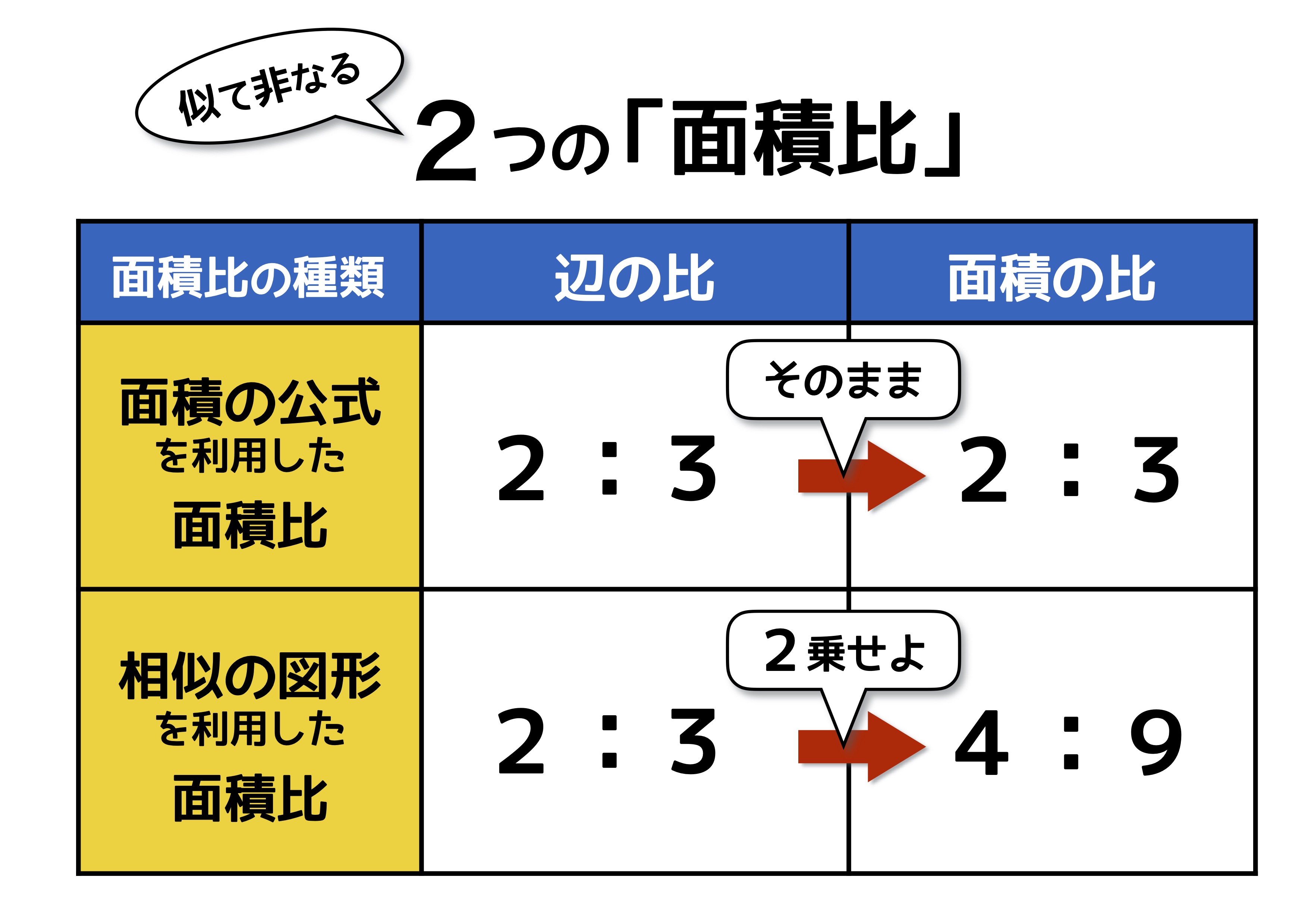



中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ



三角形の辺と面積の比 父ちゃんが教えたるっ




3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく



Mathematics 相似 4 面積と比 面積比は となりあった三角形で求める 働きアリ



面積比を辺の比として使える時と 面積比が辺の比の二乗になっている Yahoo 知恵袋




面積比 2つの三角形で高さが同じときの面積比 身勝手な主張



平面図形 辺の比と面積の比 前田昌宏の中学受験が楽しくなる算数塾




辺の比と面積比の教え方をパターンごとに解説 塾講師ステーション情報局




平面図形の苦手を解消 三角形の面積比 基本編



平面図形 辺の比と面積の比 前田昌宏の中学受験が楽しくなる算数塾



面積比




平面図形の苦手を解消 三角形の面積比 基本編



メネラウスの定理 最終奥義 高校数学の無料オンライン学習サイトko Su




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ




三角形で面積比と底辺の比の関係は 平面図形分野の頻出問題を考える みみずく戦略室



辺の比と面積比 等角三角形 富士山型 Next Stageのブログ



Newみんなの算数講座86 三角形を全部見てはいけない 中学受験の算数知恵宝庫




数a 重心 辺の比 面積比 Youtube



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生




図形の面積比 知っている人は5秒以内には解ける面積比の裏技 Youtube




数学 最重要 高さ共通 と 相似 面積比 集中特訓 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



相似とは 三角形の相似条件 記号 相似比 面積比 証明問題 受験辞典




辺の比 面積比 相似 16年東京都 高校入試 数学 良問 難問



Studydoctor相似比と面積の計算 中学3年数学 Studydoctor



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生




平面図形をマスター 三角形の面積比 応用編その3



面積と辺の比の関係を解説 図形の面積と辺の比の関係はテントやドリルで面積を求める



面積比を辺の比として使える時と 面積比が辺の比の二乗になっている Yahoo 知恵袋




算数図形編 面積比 線分比 相似 面積比を辺の長さで表そう 中学受験 高校受験パスナビ



相似比と面積比と体積比の関係を解説 公式を使って面積や体積を求めよう




小学6年生 算数 10月 辺の比と面積の比 速さ 1 練習問題プリント 栄光ゼミナール ちびむすドリル 小学生学習教材 スペシャルコラボ



三角形の辺と面積の比 父ちゃんが教えたるっ



なぜ相似比をつかって面積比が計算できるのか Qikeru 学びを楽しくわかりやすく




数学 面積比と線分比をシッカリわかると チェバの定理を深く理解できるよ 平面図形 中学数学 高校数学 行間 ぎょうのあいだ 先生



三角形の面積比を求めよう 底辺比と相似比を使えば複雑な問題もスッキリ解決 中学受験ナビ




面積比の公式まとめ 相似比と面積比と体積比の関係もあわせて解説 遊ぶ数学




辺の比と面積 平面図形 中学受験の算数 理科ヘクトパスカル




平面図形をマスター 三角形の面積比 応用編その3
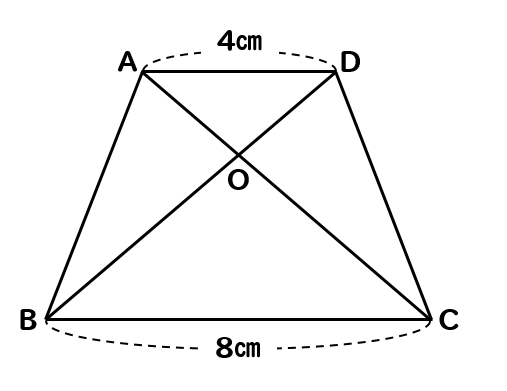



相似 台形と面積比の問題を徹底解説 数スタ



長さ比から面積比の求め方 算数解法の極意



3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく



辺の比と面積の比 中学から数学だいすき




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ



1



三角形の面積 辺の比




Helpful Site For Study 2月 18
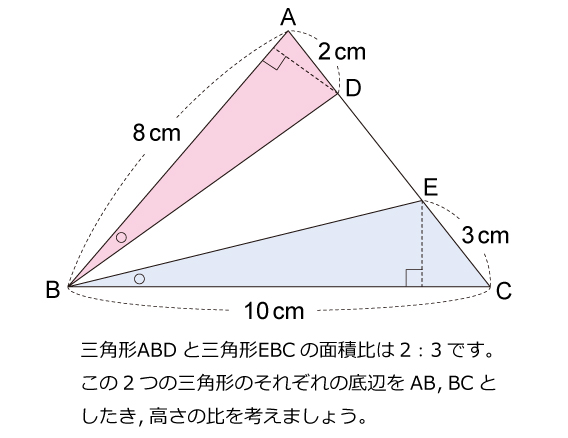



図形ドリル 第228問 等しい角度と辺の比 算数星人のweb問題集 中学受験算数の問題に挑戦
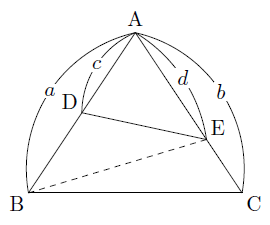



1角共有の三角形の面積比 まなびの学園



平面図形と比 2 中学受験 田中貴 Com




高校数学a 三角形の面積比 等高 等底 等角 受験の月



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生



1
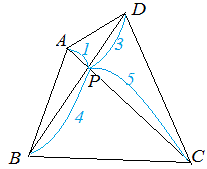



面積比



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生
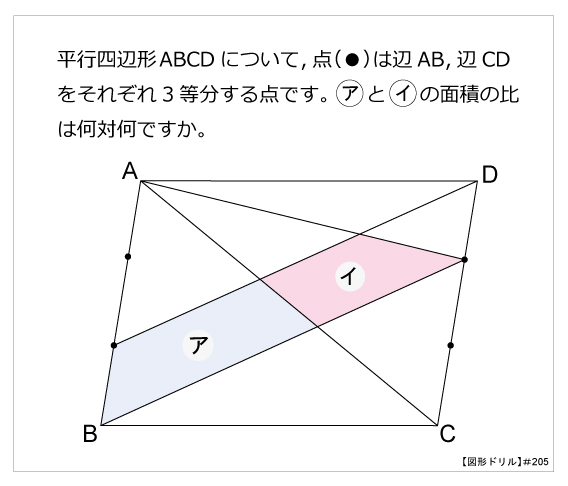



図形ドリル 第5問 平行四辺形内の面積比 算数星人のweb問題集 中学受験算数の問題に挑戦




大至急です 相似 面積比の問題です Clear



0 件のコメント:
コメントを投稿