こんにちは、ウチダです。 今日は数学a「図形の性質」で習う 「三角形の内心」 について、性質の証明や基本的な使い方(角の二等分線と比)、座標の求め方や位置ベクトル表示などをわかりやすく解説していきたいと思います。 外心に関する記事と内容がかなり似ているため、こちらの記 2つの円の位置関係は5通り あり,中心間の距離と半径によって状況が変わってくるのでどのパターンなのか把握することが重要です。このページでは5通りの分類,交点,接線,相似の中心について整理します。 → 2つの円の位置関係2 次関数の相似比と相似中心 実数係数の2 次関数はすべて相似あるいは合同であり, たとえば, =y ax 2 と =y bx 2 の相似比は b a a b 1 1 = である。 ここで,a>0 ,b>0 の場合を考え,その相似比を求めてみる。 x y O A A ' B B ' y = ax 2 y = bx 2 X Y X ' Y '
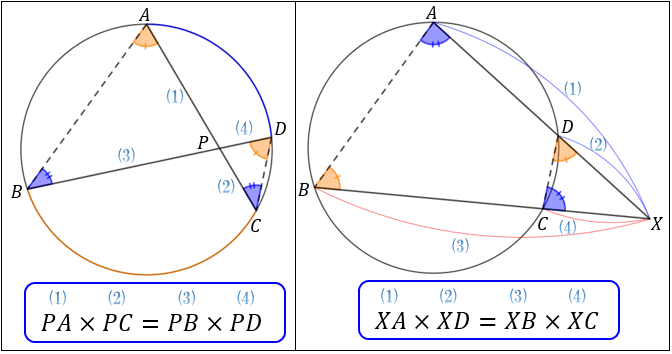
方べきの定理とは 3つのパターンの図解とその証明方法 アタリマエ
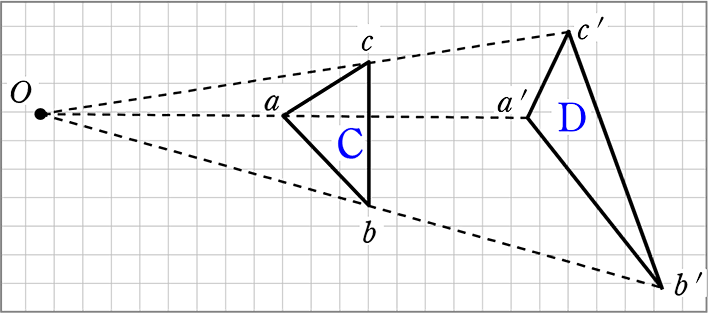
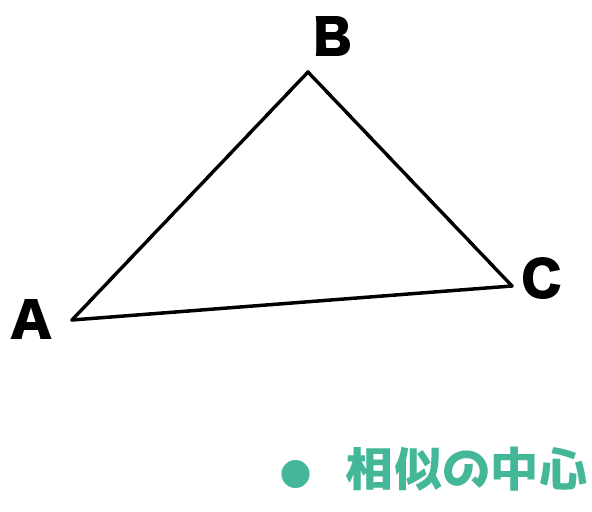
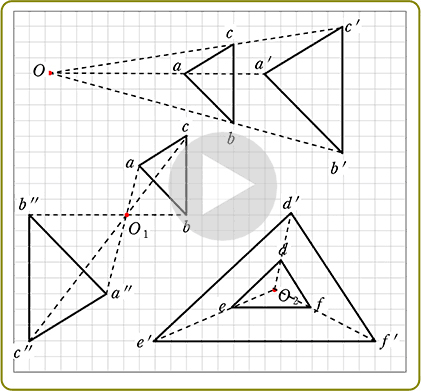
相似の中心の求め方
相似の中心の求め方- 相似*円周角*三平方の定理などの高校で習う公式 (中3が使いやすいように改良笑)や自己流に編み出した公式集 ( ´ ` )ノ 自分用に作ったので見やすさは重視してません (=゚ω゚)ノ 数学 暗記 裏技 公式 円周角 三平方の定理 面積求め方 円錐 相似な図形10 『相似』! なら「対応する辺」と「順番」さえ合っていればよい ① 2つの三角形が『相似』だった場合、ある辺の長さを求めるための表現は 実は自由です このあと「平行線と線分の比」や「方べき」などで 「この辺」:「この辺」は「この辺




接する2つの円の相似の中心 高校数学の美しい物語
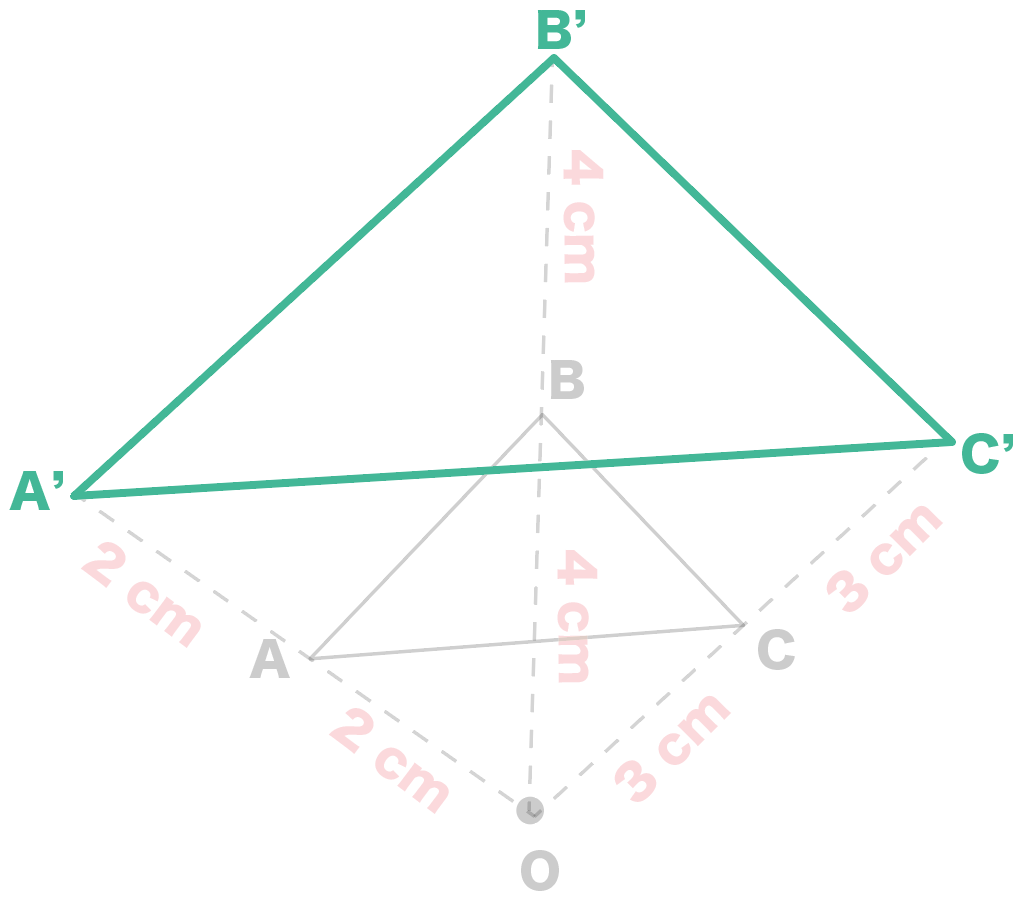
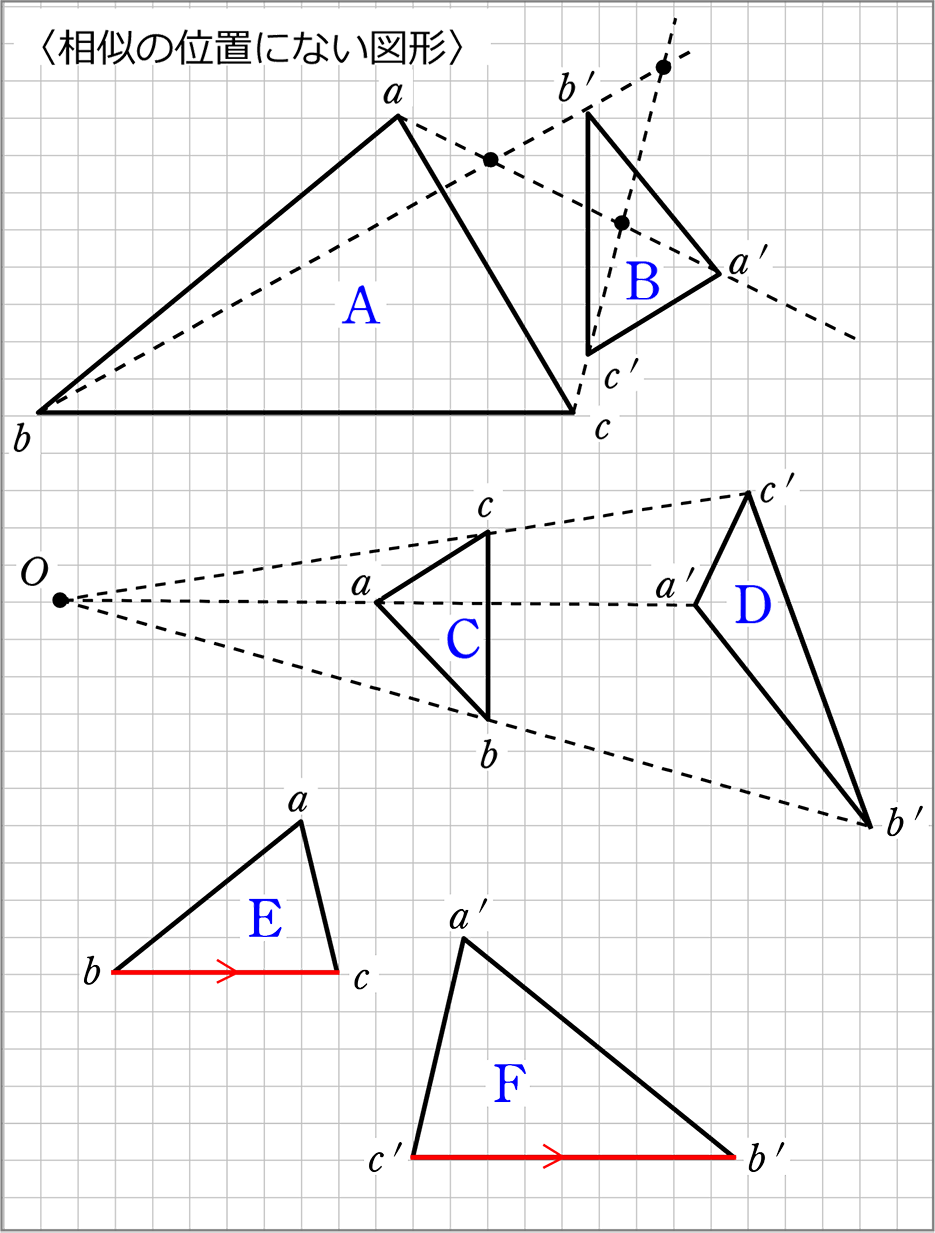
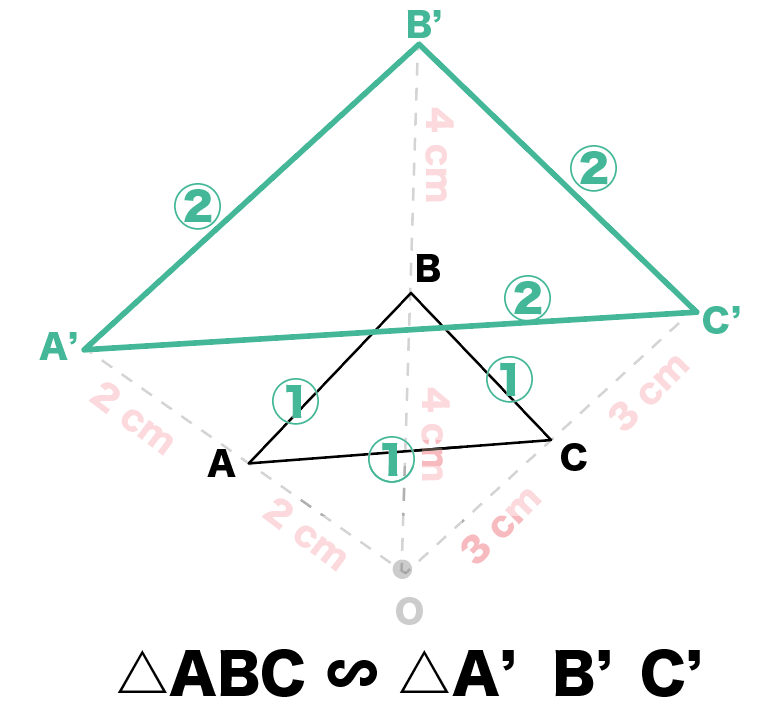
これらは、どちらも同じ相似比なので等しい比です。 より、 1 x = (1x) 1 1 x = ( 1 x) 1 が成り立ちます。 内項の積と外項の積が等しいので、 x(1x) = 1 x ( 1 x) = 1 この 2 2 次方程式を解きます。 x2 x− 1 = 0 x 2 x − 1 = 0 x = −1±√12 −4×1× (−1) 2×1 x = − 2つの図形の対応する点どうしを通る直線が 全て1点に集まり、 その点から対応する点までの距離の比が全て等しいとき それらの図形は、その点を相似の中心として、 相似の位置にある1. 1次変換(線形変換)とは (1) 写像のうちで同一集合から同一集合への対応となっているものを 変換 といいます. (2) 平面上の点 (x, y) を点 (x', y' ) に移す変換 f が次の式で表されるとき,この変換 f を 1次変換(線形変換) という. f x'=axby ・・・①
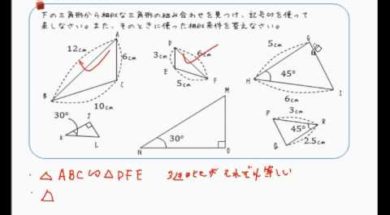
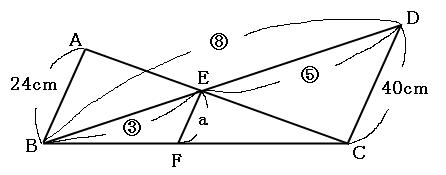
さを求めなさい。 このような出題された時に, この垂線の長さを求めるのに相似を使う方がいると思います。 ただ, 三角形の面積の求値式に目をつけると相似などという難しい技は必要ありません。 すなわち以下の解法で垂線の長さxcmを求めることが可能相似の考えを用いて,間接的に高さや 距離を求めることができる。 〇相似の考えを用いた間接的な高さや距 離の求め方を理解している。 活用力 主体性 コミュニケー ション能力 ・観察 ・ノート ・発表 整 理 ・ 分 析 三 直 4 角形 の1辺に平行なただし,(*3)の方が「相似比」に対応しており,面積比の問題への応用が楽なので(*3)の方が有利だと考えられます.(筆者の手元にある中学校の教科書はいずれも(*3)の形で書かれています) ① 円 O の半径が 10 cm であるとき,線分 CP の長さを求め
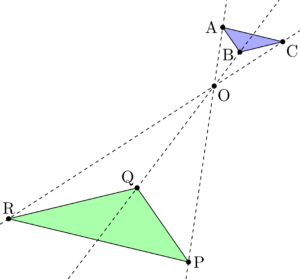
数学三角錐の体積比を楽に求められる公式 ~受験の秒殺テク(2)~ キーワードは"ちぢみ率" 高校受験を控える中学3年生の皆さんに、わずかな時間で正解を出すことができる"秒殺テクニック"を紹介していきます。手がかりが少ない 2つの円の相似の中心oを、図示しなさい。 ので、生徒の学習 (対応する点が見つ 状況をみながら取 けみくい)場合 り組ませたい。 対応する点の決め 方で、様々な解法 を見いだすことが できる。 2つの中心を通る中心線上に、相似の相似1 四角形ABCDと四角形EFGHは相似の位置にある。このとき相似の中心Oを求めなさい。 a b c d e f g h 相似な三角形を記号∽を




相似な図形や中心の作図 中3数学 Youtube




中学数学 よく出る円と相似の融合問題 Pikuu
中心に回転すると、2つの図形を重ね合わせることができる. 不動点の位置を作図する方法は,一般的にはコンパスと定規で求められる.正方形の各頂点を a,b,c,d , 移動後の正方形の頂点を a',b',c',d' としたとき,線分 aa' の垂直二等分線と,線分 bb' の垂直 相似の中心の求め方。 y=3(x1)^22(i) y=5(x2)^23(ii) 頂点は (i)P(1、2) (ii)Q(2、3) 相似の中心R(x、y) 相似比は(i)(ii)=53 RPRQ=53 よって内分の公式より ・(2x3×1)/(32)=2 ・(2y3×2)/(32)=3 以上より R(7/2、9/2) であってますか?(数学的な見方や考え方) (3)相似な図形の性質を用いて、拡大図や縮図をかいたり、線分の長さや図形の面積、体積 を求めたりすることができる。 (数学的な技能) (4)相似な図形の意味や性質について説明することができる。
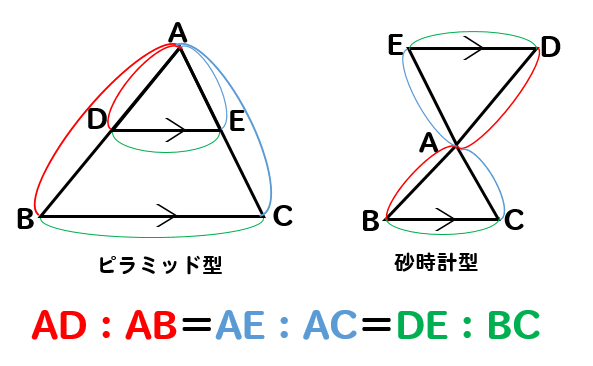



相似 平行線と比の利用 辺の長さを求める方法をまとめて問題解説 数スタ




高校数学a 方べきの定理3パターンの証明と三角形の相似 受験の月
〇相似の考えを用いて,間接的に高さや 距離を求める方法を考えることができ る。 相似の考えを用いて,間接的に高さや 距離を求めることができる。 〇相似の考えを用いた間接的な高さや距 離の求め方を理解している。 主体性 コミュニケーここで,三平方の定理の応 用として問題p をとらえると,式(1) に代入 するだけで問題が解決できる。従って,今回 のように相似の応用とした方が証明も必要と なるので,この扱いの方が適切であると考え た。また,5では,同じように相似を用いた回転移動の中心作図まとめ 回転移動した図形は 対応する点と中心を結ぶとそれぞれの線分の長さが等しくなります。 よって、それぞれの対応する点の垂直二等分線を作図し、その交点を求めることで回転移動の中心を作図することができます。



中学数学 図形の相似



平面における変換
・線の長さや角の大きさを使う書き方。 ・相似の中心 一つの点を中心として。 ③縮図の利用 地図や建物の実際の距離を求めたりする。 ④学びを活かそう 木の高さ、紙の大きさ、くもの巣などを求める。 ⑤確かめ 縮図と拡大の単元の前後例として,中心が (0, 0) (0,0) (0, 0) で半径が 2 2 2 の円の方程式を考えます。以下のおうぎ形について中心角を求めなさい。(ただし円周率は314とします。) (1)半径10cmで弧の長さが157cm 基本的な解き方 「半径が等しいおうぎ形のポイント」を利用した解き方 360×157/628=90 答え 90 ° 工夫した解き方
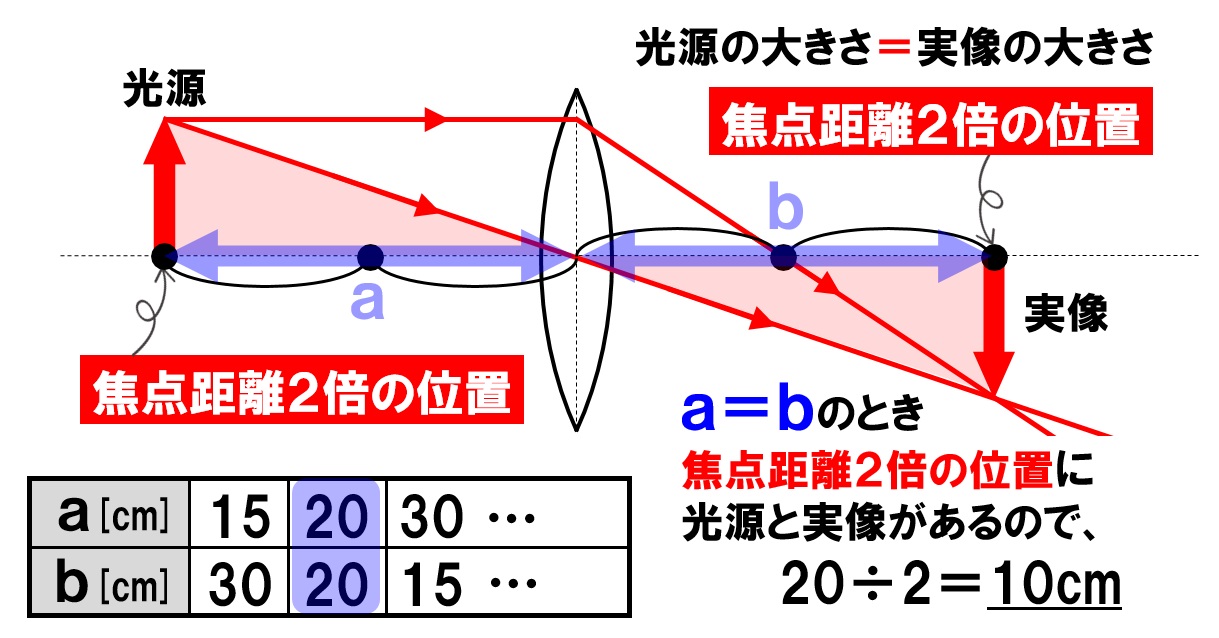



中1理科 焦点距離の求め方 作図や公式での求め方まで Pikuu
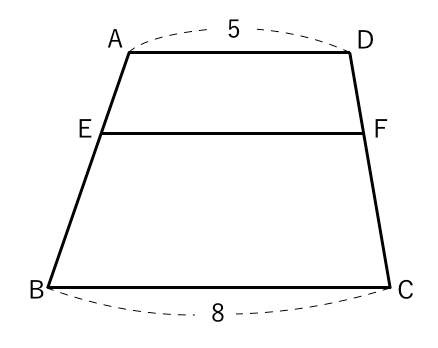



相似な図形 計算 台形 練習問題 苦手な数学を簡単に
手がかりに縮尺を求め,それ をもとに実際の長さを求め ることができる。 航空写真をもとに,校 庭にかかれた陸上のト ラックの1周の長さを 求める。 関相似な図形の性 質に関心をもち,それ について考えようとし ている。 2 1相似な 図形 ①相似な円錐の側面積、底面積、表面積の求め方 😙 いずれにしても、これらの体積や表面積を計算できるようにならなければいけません。 そしてこの弧の長さを使えばおうぎ形のつまり側面の中心角、ひいては面積を出すことができます。 円錐問題の考え方5 三角形の相似条件を用いて,簡単な図形の性質を証明することができる ア-② ようにする。 イ-③ 6 相似の位置の意味を理解し,拡大図・縮図をかくことができるようにす ウ-④ る。 7 縮図を利用した高さや距離の求め方について考えさせる。




相似な図形 Ict教材eboard イーボード




中3数学 円と相似 の証明問題の解き方のコツ 映像授業のtry It トライイット
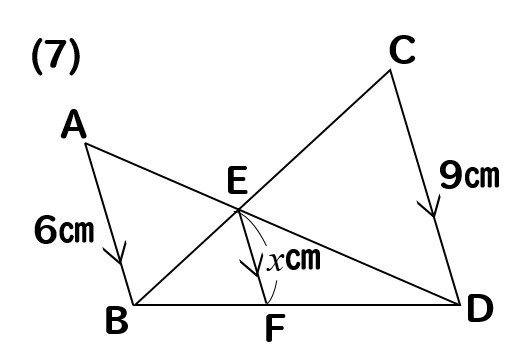
問題1と完全に同じ求め方により、\(21cm\) と求まります。 ここまで求めた状態から、次に上の小さい球の半径を求めます。 下の図のようになっています。 この図における相似な直角三角形たちは、 \(3\) 辺の比が \(\) であり、 コンパスの針が中心,針から鉛筆までの距離が半径になります。 円の方程式の求め方 円の定義をもとに円の方程式を考えます。 中心が原点の場合の円の方程式; 相似な図形の見つけ方、相似条件とは? 平行線と比の利用、辺の長さを求める問題をパターン別解説!←今回の記事 木の高さを求める方法について解説! 中点連結定理を使った問題を解説! 相似の面積比を求める問題をイチからやってみよう! 面積比!



Http Www Kumamoto Kmm Ed Jp Sugakubraindumps Pdf 3 5 Answer Pdf




接する2つの円の相似の中心 高校数学の美しい物語
この変換を中心相似対称変換という. ことにより点s,pを求めることができるので,両側に平行移動することにより 4点p,q,r,sが求められるとしてもよい. この例が示す通り,変換を用いた解答はどれも面白いものばかりです. 時間をかけていろいろな問題相似の基本は三角形にあることを理解させる。 (2) 様々な考え方ができる問題を与え,考え方を深めさせる。 (3) 生徒の意見をできる限り取り上げることで生徒の考え方のよさを見出し,解ける喜び,発見できる喜びを味わわせる。




中学数学 図形の相似




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ
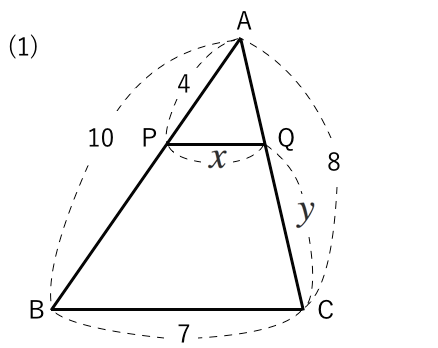



相似な図形 長さを求める 苦手な数学を簡単に



平面における変換
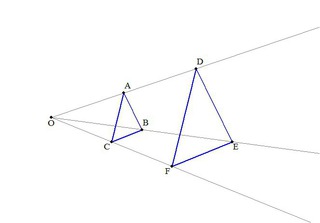



中学校数学 3年生 図形 相似な図形 Wikibooks
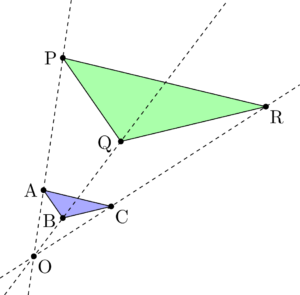



すべての放物線が相似であることの証明 大学入試数学の考え方と解法




中3 相似の中心を利用した作図 Youtube
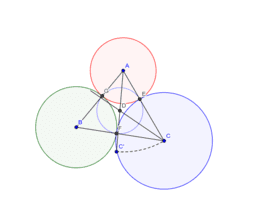



アポロニウスの問題 Geogebra




相似な図形 計算 台形 練習問題 苦手な数学を簡単に
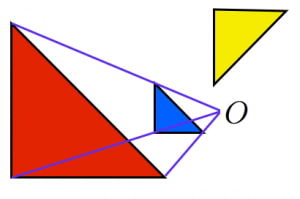



全ての放物線が相似であることの証明 高校数学の美しい物語
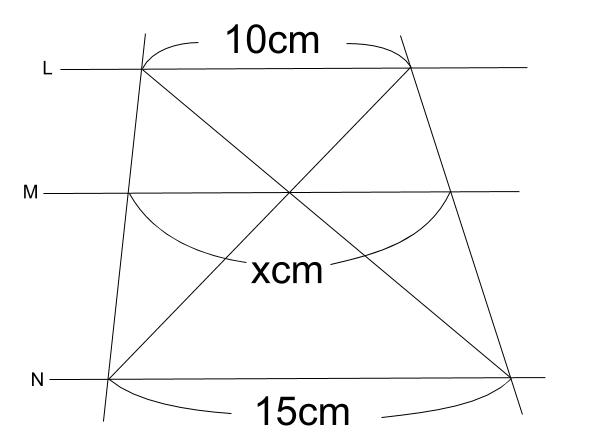



中学数学 平行線と線分の比 その2 中学数学の無料オンライン学習サイトchu Su
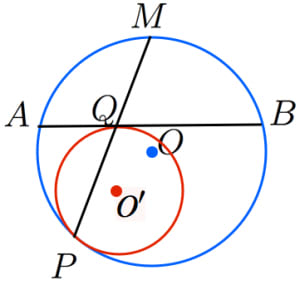



接する2つの円の相似の中心 高校数学の美しい物語



簡単作図 相似の中心を使って拡大図をかく5つのステップ Qikeru 学びを楽しくわかりやすく



四角形a B C E は点oを相似の中心として四角形abcdを2分の Yahoo 知恵袋




相似の中心と作図 Youtube




簡単作図 相似の中心を使って拡大図をかく5つのステップ Qikeru 学びを楽しくわかりやすく




中3 相似の中心を利用した作図 Youtube
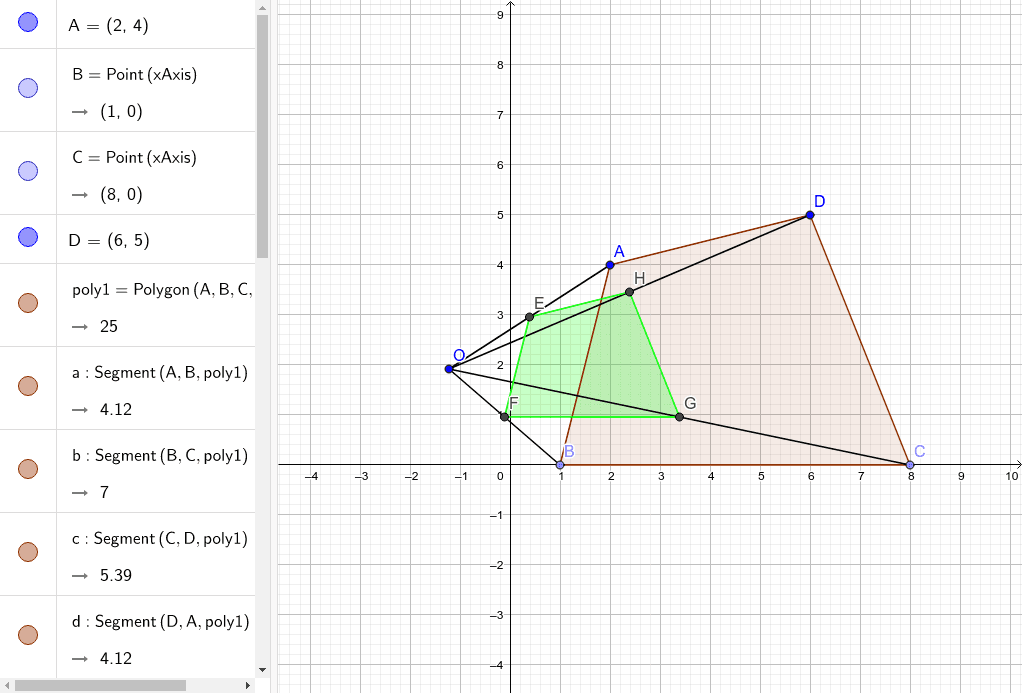



相似の中心の移動 Geogebra




作図 線分の3等分 中学数学の無料オンライン学習サイトchu Su




相似の中心と作図 Youtube



1



ある図形と相似な図形を作図する時 相似の中心はどこに作っても作図 Yahoo 知恵袋




中学数学 中学流 に外接円の半径を求める ジャムと愉快な仲間たち 0名




Nitter



Www Pref Hiroshima Lg Jp Uploaded Attachment Pdf




相似な図形 補助線を引いて考える相似の問題 中学生からの勉強質問 数学 進研ゼミ中学講座
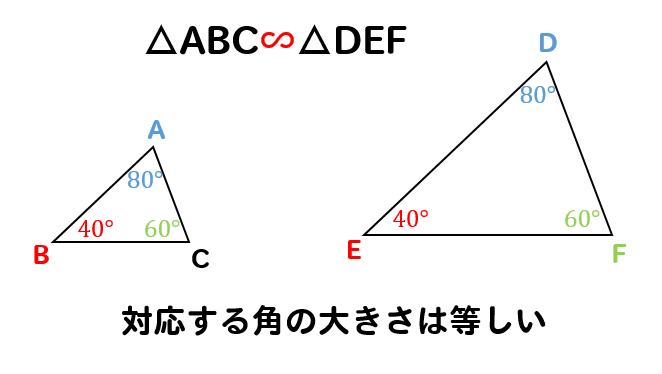



中3数学 相似の基本性質をわかりやすく問題解説 数スタ
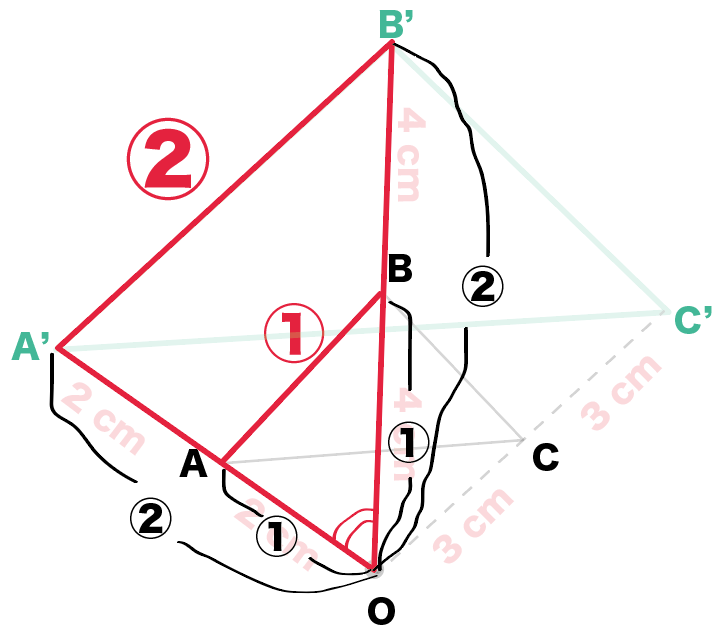



簡単作図 相似の中心を使って拡大図をかく5つのステップ Qikeru 学びを楽しくわかりやすく
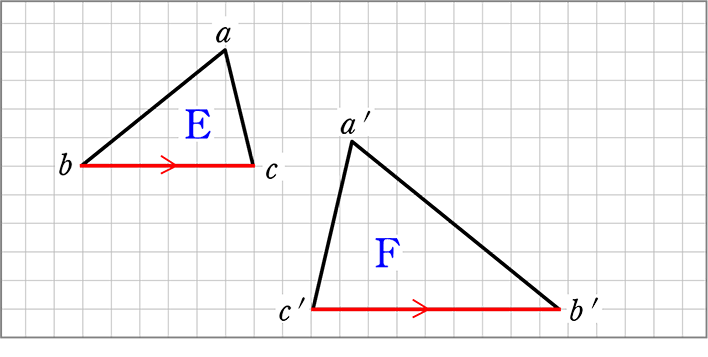



中学数学 図形の相似



相似の位置 相似の中心とはなんですか 2つの図形の対応す Yahoo 知恵袋




相似 作図 この問題の解説の 赤丸ぶぶんがよく分からないです Clear
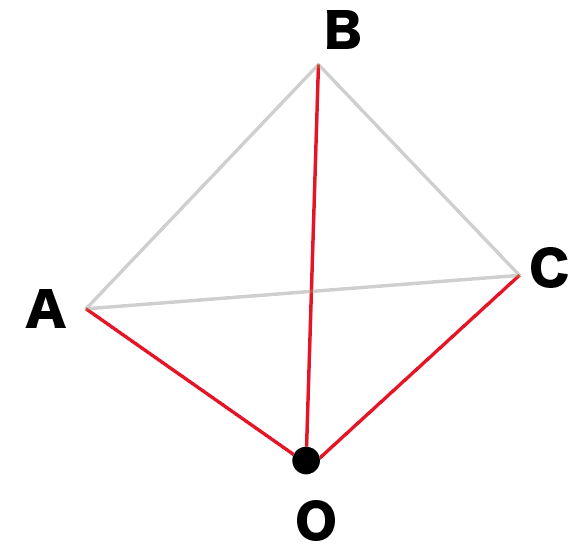



簡単作図 相似の中心を使って拡大図をかく5つのステップ Qikeru 学びを楽しくわかりやすく
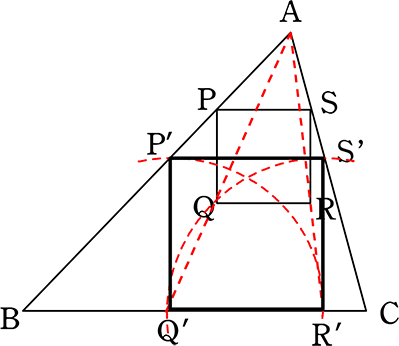



中学数学 図形の相似




中3数学 拡大図 縮図の作図 映像授業のtry It トライイット




表面積と体積の比の問題 立体の相似比を出すのが一番最初だ 中学や高校の数学の計算問題



Http Www Pref Chiba Lg Jp Kyouiku Shidou Gakuryoku Yaruki Suugaku Documents M3012 Pdf



相似の中心 中学から数学だいすき



中学3年 数学 相似の中心と作図 Cmovie 教育に特化した無料動画サイト シームービー オンライン学習サイト



Http Www Asahikawa Hkd Ed Jp Asahi Els 13 Seien Suugaku30 Pdf



Http Www2 Gsn Ed Jp Houkoku 03c 03c07 03c08s Pdf



簡単作図 相似の中心を使って拡大図をかく5つのステップ Qikeru 学びを楽しくわかりやすく




中3 中学3年 数学 相似と比 円周角と中心角 中学生 数学のノート Clear



Studydoctor相似な図形や中心の作図 中3数学 Studydoctor




ぬるいパースが描けるようになりたい 共通外接線 共通内接線の描き方




相似の位置と中心 中3数学 Youtube



Http Www Rs Tottori U Ac Jp Mathedu Mathedu Journal17 Files 17 01 Pdf



中学数学 図形の相似



中学生 アーカイブ Cmovie 教育に特化した無料動画サイト シームービー オンライン学習サイト



相似 平行線と比の利用 辺の長さを求める方法をまとめて問題解説 数スタ




方べきの定理とは 3つのパターンの図解とその証明方法 アタリマエ



相似下の方顔用紙に四角形abcdを点oを相似の中心として 2倍に拡大した四 Yahoo 知恵袋



相似の位置 相似の中心とはなんですか 2つの図形の対応す Yahoo 知恵袋




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ



Http Www2 Gsn Ed Jp Houkoku 03c 03c07 03c08s Pdf




動画で学習 3 相似の位置 数学



作図 相似の中心の利用 中学数学の無料オンライン学習サイトchu Su



1



中学数学 図形の相似



相似の位置 相似の中心とはなんですか 2つの図形の対応す Yahoo 知恵袋




三角形の相似条件 証明の練習になる簡単な問題を紹介 中学や高校の数学の計算問題



Studydoctor平行線と台形 中3数学 Studydoctor



平面における変換



作図 相似の中心の利用 中学数学の無料オンライン学習サイトchu Su



数学の相似の図形の問題です分かる方 この問題の答えを教えてくださいこの Yahoo 知恵袋



相似の中心 中学から数学だいすき




中3数学 相似な図形の見つけ方 相似条件とは 基本問題を使って解説 数スタ



Http Www Rs Tottori U Ac Jp Mathedu Mt Xue Sheng Zuo Pin Files J3 Pdf



相似な図形の問題の解き方を解説 相似は隠れたチョウチョとトンガリを探すべし



Http Www Criced Tsukuba Ac Jp Renkei Msa Lessonplan Ooneda 2nd Medio Ooneda07 Jap Pdf



ある図形と相似な図形を作図する時 相似の中心はどこに作っても作図 Yahoo 知恵袋




相似の中心となる点について 相似の中心となる点についてこんにちは 数学 教えて Goo



Studydoctor相似の位置と中心 中3数学 Studydoctor



Http Toitemita Sakura Ne Jp Suugakukonetapdf Nijikannsuu Soujityuushin Pdf
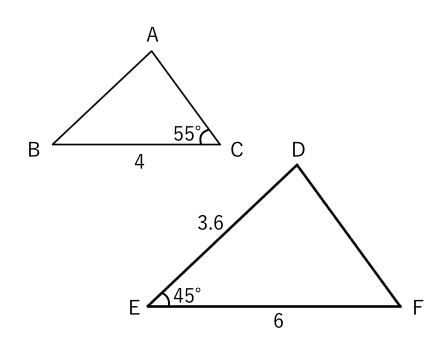



相似な図形 確認問題 苦手な数学を簡単に
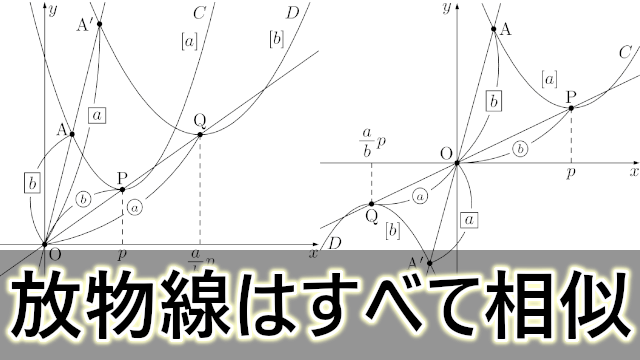



すべての放物線が相似であることの証明 大学入試数学の考え方と解法
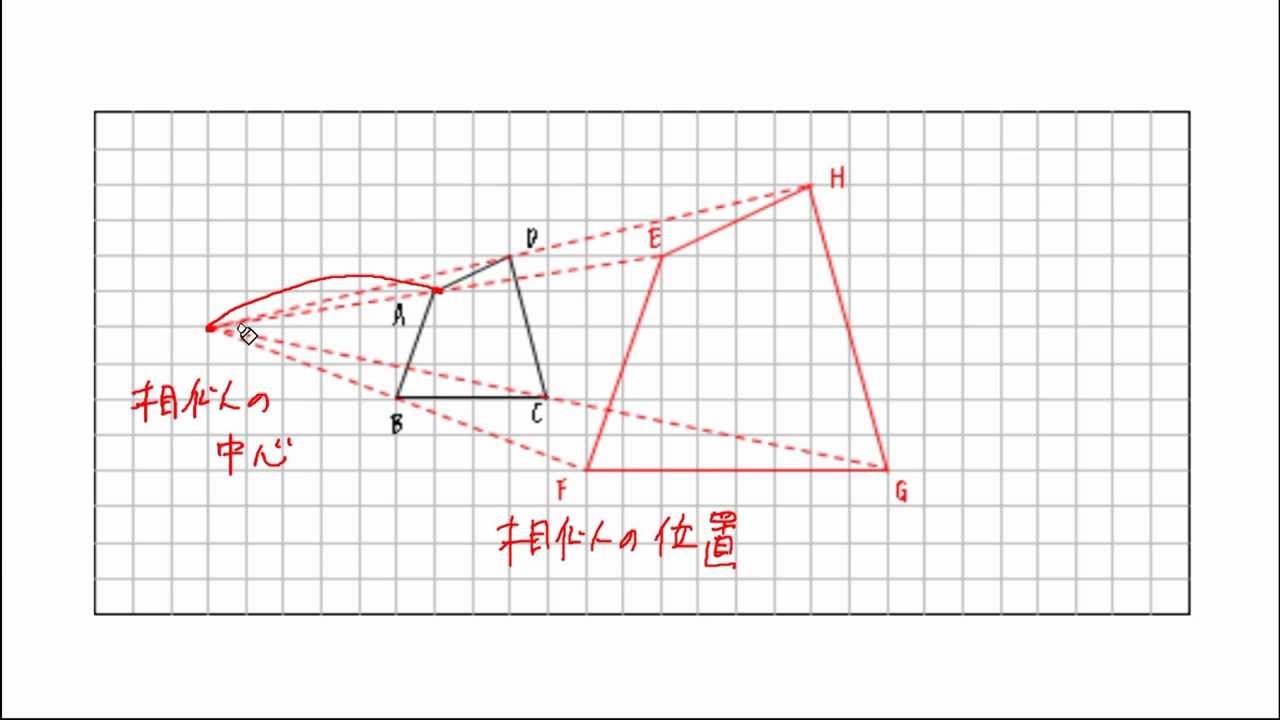



相似の中心と作図 Youtube




相似の利用 木の高さを求める方法を問題解説 数スタ
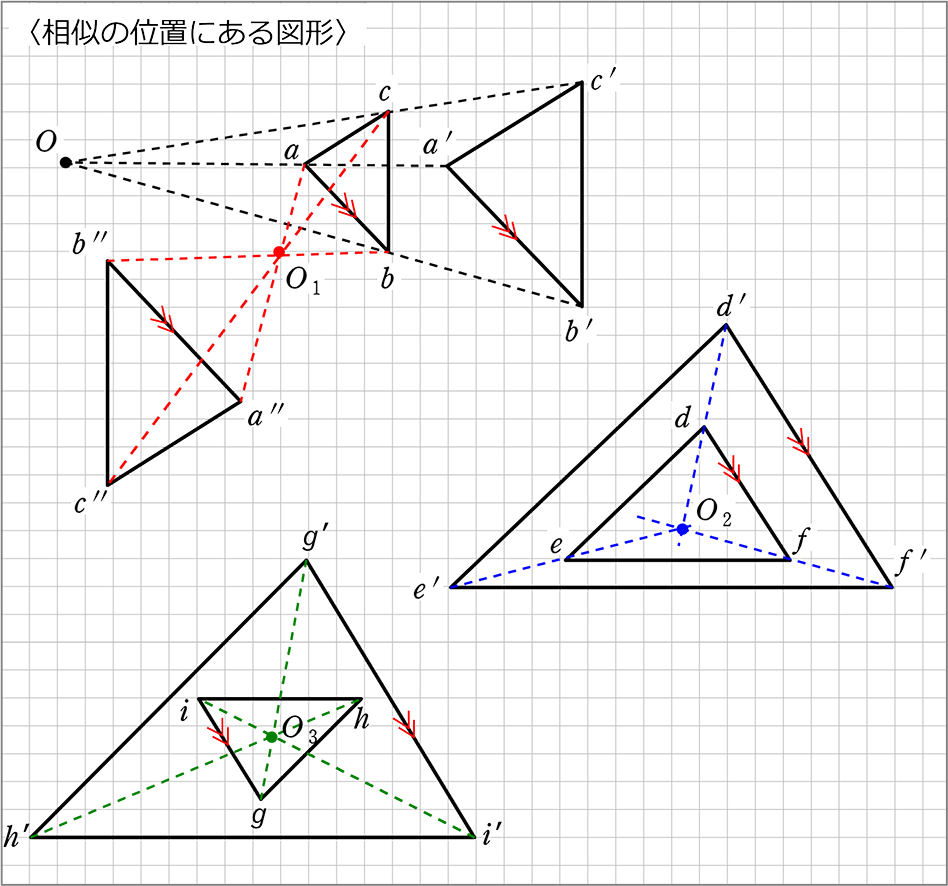



中学数学 図形の相似




相似 作図 この問題の解説の 赤丸ぶぶんがよく分からないです Clear



すべての放物線が相似であることの証明 大学入試数学の考え方と解法
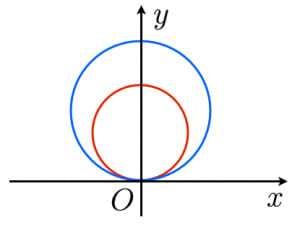



接する2つの円の相似の中心 高校数学の美しい物語



中学校3年 数学 アーカイブ Cmovie 教育に特化した無料動画サイト シームービー オンライン学習サイト



中3の数学です 円の縮図の書き方がわかりません 点oを相似の中心 Yahoo 知恵袋



中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



相似の中心と作図 Youtube
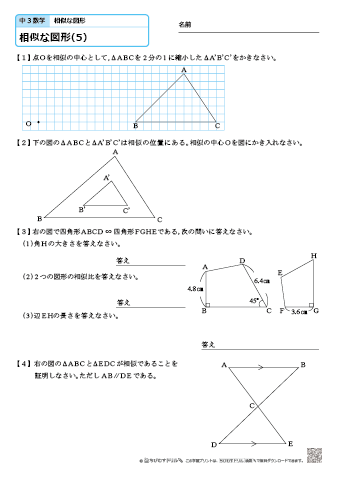



中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
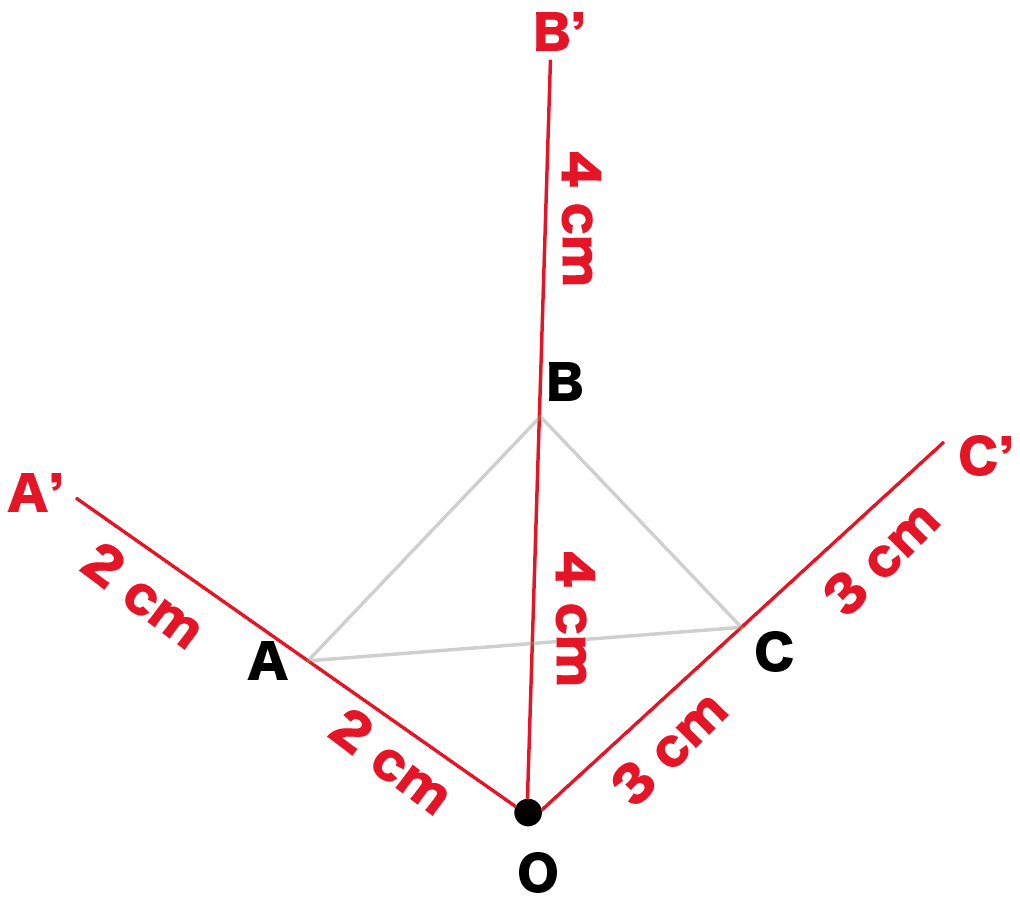



簡単作図 相似の中心を使って拡大図をかく5つのステップ Qikeru 学びを楽しくわかりやすく
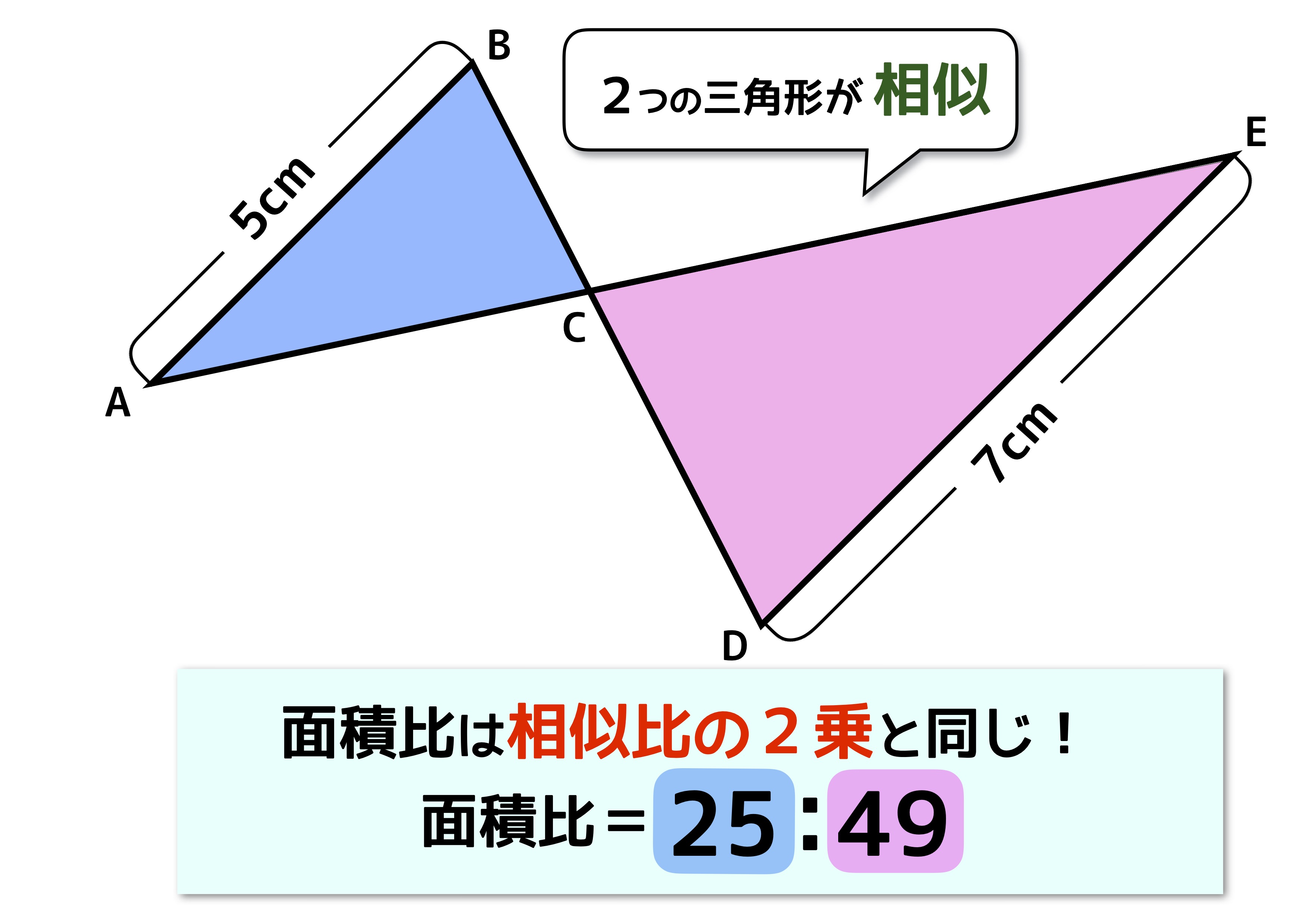



中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ



簡単作図 相似の中心を使って拡大図をかく5つのステップ Qikeru 学びを楽しくわかりやすく



平面における変換



0 件のコメント:
コメントを投稿